In most cases, when we choose "Factor Analysis" on an analyzing software, the method of extracting the default factor is either [Principal Component Analysis] or [Factor Analysis]. However, though being mathematically similar, the fundamental idea of a factor analysis and a principal component differs completely.
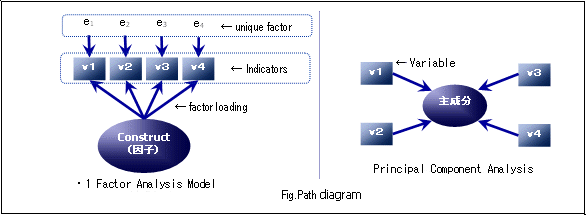
There are two models to a Factor Analysis. One, which looks into indicators based on unmeasured common factors, and two, a model which analyzes based on unique factors other than the common factor. Common factors here are defined as a Construct, which makes describing or interpreting principles, phenomena, or problems much easier. For example, when we have indicators (questions, which will be asked to respondents at surveys) such as 1) one month of allowance 2) numbers of favorite foods 3) Engel's coefficient, "quality of life," the unmeasured underlying potential common factor could affect the three indicators. However in reality what affects indicators are not merely its quality of life. A character obsessed with high-end brands, craving products regardless of his/her economical status could also be an underlying factor for the indicator 2), numbers of favorite food. As explained, the model explains factors unable to be explained just by common potential variables as error variables (unique factor). Factor Analysis is a method of analysis where the principal aim is on the affects underlying in common factors (underlying variable).
On the other hand, the Principal Component Analysis is the complete opposite, and involves taking combined variables as the gprincipal componenth from different indicators, forming a linear combination, and analyzing the overview of entire data. The large difference between the two methods is existence or non-existence of error variables (unique factors), and the correlation of cause and effect between indicators and underlying variables.
The [Factor Analysis]-[Factor Extraction Method:Principal Component Analysis] involves setting initial values as 1(unique factor as 0) and making presumptions based on the Principle Factor Method. (Therefore, if factors are not rotated, this corresponds with the result of Principal Component Analysis, analyzed based on correlative matrix) Perfect methods do not exist in Factor Analysis. Though this method is surely not incorrect, lack of mathematical basis in the initial set up of commonality (such as its minimum value) could lead to factor loading being highly estimated. How can we utilize the other options in [Factor Extraction Method]? Software nowadays has developed to a large extent and has made our lives convenient, but nevertheless there are obviously some times when we face issues using this complex tool.
Other popular basic Multivariate Analysis include Regression Analysis, Principal Component Analysis, Factor Analysis, and Discriminant Analysis. Today, various methods have been developed such as applied methods or methods using algorithm.
CBR also conducts other numerous special analysis such as:
Covariance Structure Analysis
Correspondence Analysis
Conjoint Analysis
Application of Item Response Theory etc.


