− クロス集計のみでは解釈が難しいような問題を解決したい
− より複雑な原理・現象をひも解き、理論的根拠に基づく最適な落としどころを示唆してほしい
このようなときに多変量解析は有用な手法です。
近年のパソコンやSW(ソフトウェア)の進歩は目覚しいものであり、比較的容易に多変量解析を扱えるようになりました。
ソフトウェアインターフェイスの指示されるままにオペレーションを施せばビジュアルのきれいなチャートなどが完成しますが、それは本当に適切な結果なのでしょうか?あるいは、今後の対応策を的確に示唆しているものと言えるのでしょうか。
ソフトウェアを簡単に操作できることは大変喜ばしいことですが、その理論的根拠や本質をおろそかにすることはいたずらな解釈を招きかねない危険なことだと思われます。
CBRでは背後にある理論的根拠や本質にも焦点を当て適切な分析方法を選択し、より洗練された結果のご報告を目指しております。
例えば、よくあるケースですが解析ソフトで"因子分析"を選択するとデフォルトの因子抽出方法は【主成分分析】であったり【因子分析】であったりします。ですが、因子分析と主成分分析は数理的に酷似していますが、その根本の考え方は似て非なるものです。
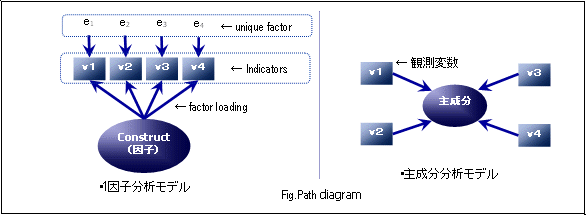
因子分析は観測変数(Indicators)を測定できない共通の要因(因子)から説明するモデルと因子以外の独自性から説明されるモデルで表現できます。ここで因子は概念の集約を表すもの(Constract)と定義され、原理・現象・問題の単純表現化、解釈のための一役を担います。例えば、観測変数(実際に調査などで対象者に質問する項目)を1)1ヵ月のおこづかい、2)嗜好品の所有数、3)エンゲル係数 としたとき、この背後には"生活水準の高さ"という共通の観測できない潜在的な要因が存在し、この高低が1)-3)の観測変数に影響を及ぼしていると捉えることができます。しかし、実際には観測変数への影響はこれだけではなく、例えば嗜好品の所有数ならば、ある人はブランド志向が強く、たとえ生活が苦しくとも自分が好きなものを揃えたいという要因も存在するかもしれません。このように共通的な潜在変数だけでは説明できない要因を誤差変数(独自性:unique factor)としてモデルを表現します。因子分析は背後にある共通的な要因(潜在変数)からの影響具合(因子負荷量:Factor loading)に主眼を置いた分析です。
一方、主成分分析はその逆に近い考え方で、いろいろな観測変数から“主成分”とする合成変数を線形結合により生成して、データ全体の状態を見渡すことを主目的とします。両者の大きな違いは誤差変数(独自性)の有無と観測変数と潜在変数(因子)間の因果の方向です。
[因子分析]-[因子抽出方法:主成分分析]とは、共通性の初期値を1(独自性を0)に設定して主因子法で推定する方法です。(つまり因子の回転をかけなければ、相関行列を分析元とする主成分分析の結果に一致します。)
因子分析に万能な方法というものは存在しません。共通性の初期設定(その下限値は知られています)には何ら数理的根拠は存在しないので、もちろんこの方法でも間違いとは言えませんが、因子負荷量が高めに見積られてしまう可能性も否めないのではないでしょうか。また、この[因子抽出方法]の中にあるその他のオプションはどのような時に使えば良いのでしょうか・・? このようにソフトウェアは発達して便利になりましたが、使い方に戸惑ってしまうケースも多いのではないでしょうか。
Basicな多変量解析としては、回帰分析、主成分分析、因子分析、そして判別分析などが有名です。現代においては、これらの手法の応用形や新たなアルゴリズムを導入した多種多様な手法が考案されております。 ここでマーケティング調査でしばしば活用される多変量解析のいくつかの手法をご紹介致します。
1. コレスポンデンス分析
コレスポンデンス分析は2つのカテゴリカル変数の相互関係を解析することが主目的で、例えば「ブランド x エクイティ」などのマッピングなどによく使われます。この手法はフランスから端を発し、日本では「対応分析」と呼ばれております。 一方、日本においてもカテゴリカル変数の分析手法は「林の数量化理論」という独自の進化を遂げ、特に「数量化理論III類」は数理的にコレスポンデンス分析と同義であることが知られています。
分析事例
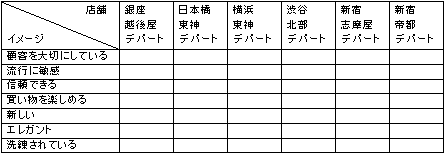
【命題】 主要百貨店(仮想)がどのようなイメージで捉えられているか分析する
コレスポンデンス分析は以下のようなクロス表を元に分析をかけます。従って、調査の時に店舗イメージに関する質問を設けておきます。
コレスポンデンス分析はクロス表の行列比率の反応パタンから関係性を解析します。この反応パタンは"プロフィル"と呼ばれております。ここで行、列合計の反応パタンを重みとする新たな行列を作り、とある理論的手法により情報を縮約(線形代数学に基づく特異値分解を利用)した座標成分スコアというものを算出します。この成分スコアを同時布置することにより関係性を考察します。 コレスポンデンス分析は情報を縮約し、全体の様子を眺めるという点で主成分分析と非常によく似ています。データの参照元、生成の方法が異なり、主成分分析は変数の分散共分散行列や相関行列を分析の出発点としますが、コレスポンデンス分析は変数の頻度データを出発点とします。
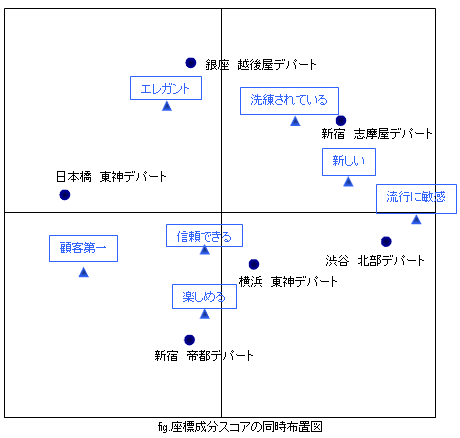
【分析結果】
行列変数の座標成分スコアを求めたところ、以下のような2次元平面に布置されたとします。この座標成分スコアは行列比率反応パタンを元に算出しているので絶対的な値の意味は持ちません。相対的な距離が関係性を表しております。コレスポンデンス分析は主成分分析などのように軸に対する解釈は通常行いません。
この事例によると、各デパート店舗はおおむねイメージ特長のところに散らばって布置されており、それぞれの個性が伺えます。例えば、銀座 越後屋デパートは高級なイメージ、新宿 帝都デパートは買い物が楽しめるといった消費者にとってより身近な存在であることが示唆されています。また、渋谷 北部デパートは流行に敏感で、常に新しいものを追い求めている姿勢であることが示唆されています。この結果からはデパートのイメージは店舗種別のみならず、地域性(土地柄)という要因も関係していると読み取ることができるのではないでしょうか。
このようにコレスポンデンス分析は、変数間の複雑な関係性を次元縮約による単純化を試み、よりわかりやすく全体を考察することができます。
2. クラスター分析
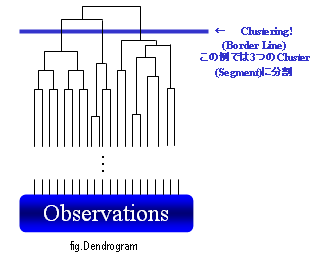
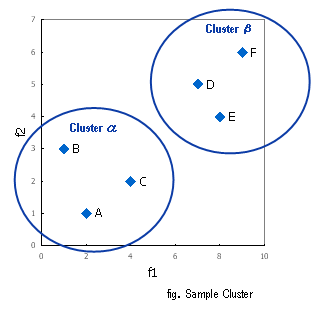
クラスター分析とは、似たもの同士を同じ仲間(Sample Cluster)として括ることを主目的としています。その"括り方"は適当に括るのではなく、様々な理論を根拠として合理的に処理しようという考え方です。括られた塊(集団)のことをクラスターと言います。クラスター分析では各々のクラスターについての特性を考察し、他の分析と組み合わせることによってターゲット・セグメンテーションなどで、その威力を発揮します。
個々のデータから"何をもって仲間とするか"の定義、観点には様々な考え方があります。例えば、"互いの距離が近い"⇒"同じ仲間(Cluster)"と捉えることができます。ここでの"距離"の概念もいろいろ考えられます。距離の定義はデータをn次元空間上に布置したときのいわゆる見た目上の距離(ユークリッド距離)を利用する場合から、確率的な考え方(互いに出現確率が高い事象は距離が近いと定義する)を導入したマハラノビスの汎距離などで規定する方法があります。従って、一口にクラスター分析と言ってもこれらのコンビネーションによりOutputもいろいろと変容し得ます。
分析手法
クラスター分析の手法は大きく2つに分類されます。1つは分類そのものに階層構造を持つ【階層的手法】、もう1つは【非階層的手法】に分けられます。代表的なものをいくつか以下にご紹介致します。
1)階層的手法…単連結法、ウォード法、重心法、..etc..
2)非階層的手法…k-means、潜在混合モデル、..etc..
階層的手法
個々のデータから上位概念のクラスターとして集約していきます。
デンドログラム(樹状図)という図でその状況が表現されます。
k-means
非階層的手法の代表的な手法で、クラスター分析では頻繁に利用されます。非階層的手法とは基準とも言うべく"評価関数"を規定して最適なクラスタリングを行う手法です。k-meansは個体とその帰属する各クラスターの中心との距離の平方和が最小となるような基準で 探索的にクラスタリングを試みます。具体的なクラスタリング方法は個体の中からk個の初期値を定めて、それ以外の個体との距離を測ります。距離が近いもの同士を同一クラスターとして括り、新たにクラスターの中心を求めます。この作業を最終的にk個のクラスターに収束するまでくり返します。
k-means法の結果は初期値の設定に依存します。得られた結果は局所最適解であり、評価関数の一般化最小値解の算出はアルゴリズム上極めて困難です。通常は初期値をいくつか変化させ、評価関数が最小のものを分析用として採用します。一般に物事の分類には様々な観点からの方法があり"これが正解クラスター"というものは存在しません。ですのでそれを短所と捉えず、より現実に即した柔軟な分類ができると前向きに捉える方が賢明と思われます。
潜在混合モデル
潜在混合モデルとは、分布の背後に確率モデルを規定して分類(クラスタリング)する考え方です。 個々のクラスターのデータ発生機構が確率分布に従い独立事象であると仮定したとき、データxの分布はその同時分布に相当します。
例えば、以下の左図は男性:女性=4:6で構成された(仮想)母集団の身長の確率分布を表したものです。男性の平均は170cm、女性の平均は160cmと仮定すると、女性の構成比率の方が多い分、若干左側の山が高くなっております。
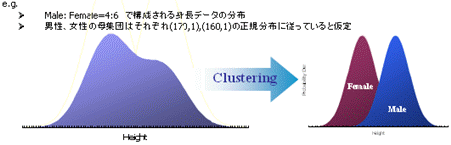
この事例では確率変数が1変数(身長)で、分別する軸も既知(性別)なので、クラスタリングは判別分析などを用いて容易に行うことができます。しかし、実際の場面では一般に変数はもっとたくさんあり、分別する軸もなにを基準としたら良いかわからない場合が少なくありません。潜在混合モデルではこの分別軸を潜在的な変数としてクラスタリングします。更に、クラスターをいくつに分ければ良いか見当がつかないことも多いと思います。潜在混合モデルは確率モデル由来のためAIC,BICといった情報量規準を参照することができます。これによりモデル全体の良し悪しが判断でき、最適なクラスター数がいくつであるかを理論的に示唆してくれます。 また、潜在混合モデルはSEMとの親和性が高く、SEMの下位モデルとして捉える考え方も発達してきております。
Fuzzy c-means
考え方はk-meansとよく似ています。k-means法では各々の個体は"Cluster αに属する"など一意に定まります。それに対してFuzzy c-meansは評価関数に0から1の連続値を取る"帰属度"という概念を置いたモデルでクラスタリングされます。つまり、"Cluster αに帰属度0.7、Cluster βには帰属度0.3 で属する。"と言うように、曖昧さを許容するクラスター分析です。
分析事例
【命題】 とあるエスティックサロンの店舗で顧客満足度を効率的に向上させるため、今後どのような人たちにどんなアクションプランを策定すれば良いか検討する。
調査の項目としては対象者の特性情報(性・年代など)をはじめ、店舗への来店状況、本人の価値観、習慣など、様々情報を収集し、クラスター分析を施しました。3つのクラスターに分類でき、それぞれの顧客タイプ別にアクションプランを策定しました。この事例ではClusterβの"潜在顧客 脈ありクラスター”と命名した集団が構成比率も高くポテンシャルも高いと予想され、満足度を効率的に上げるためにはプライオリティの高い顧客セグメントであると言えるのではないでしょうか。

ページ上へ